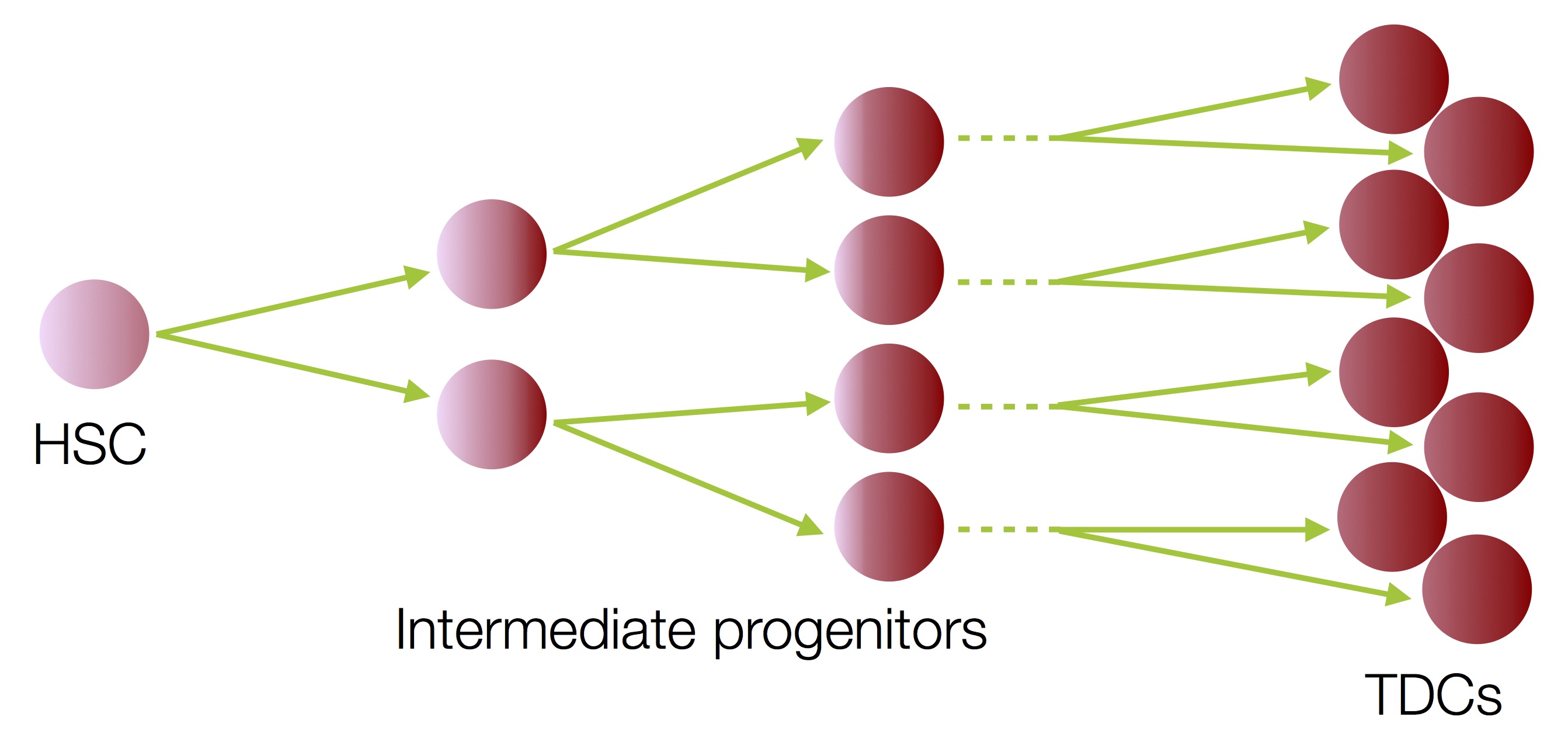
The human hematopoietic system produces 10¹¹ cells per day, which emerge from relatively rare hematopoietic stem cells. A complex division tree has evolved to allow multiple cell types to be produced and to amplify the cell numbers. This structure can also prevent the accumulation of mutations, which are inevitable given the huge number of divisions per day. By combining experimental data and mathematical models, we hope to reconstruct this tree and to understand the impact that ageing and disease have on the hematopoietic system.

This project is in collaboration with the Division of Hematology at University Hospital Zürich, and is part of a larger SystemsX.ch project between ETH Zürich, University Hospital Zürich, and University Hospital Basel.

Further sub-projects relate to the dynamics of hematopoietic stem cells, in particular how the effects of disease spread, transplantation, and host conditioning.

Cancer is a genetic disease, requiring multiple alterations to the genome to initiate uncontrolled proliferation. Mathematical models have long been used to further our understanding of this malignancy, and can help us understand cancer initiation, progresssion, and evolution. They can also inform us about the efficacy of treatment strategies, both in terms of clearance of the disease and preventing the emergence of drug resistance.

My interests here lie in understanding the initiation of cancer in stem cells and in tissue, and in treatment strategies which prevent the accumulation of drug-resistant cancer cells.

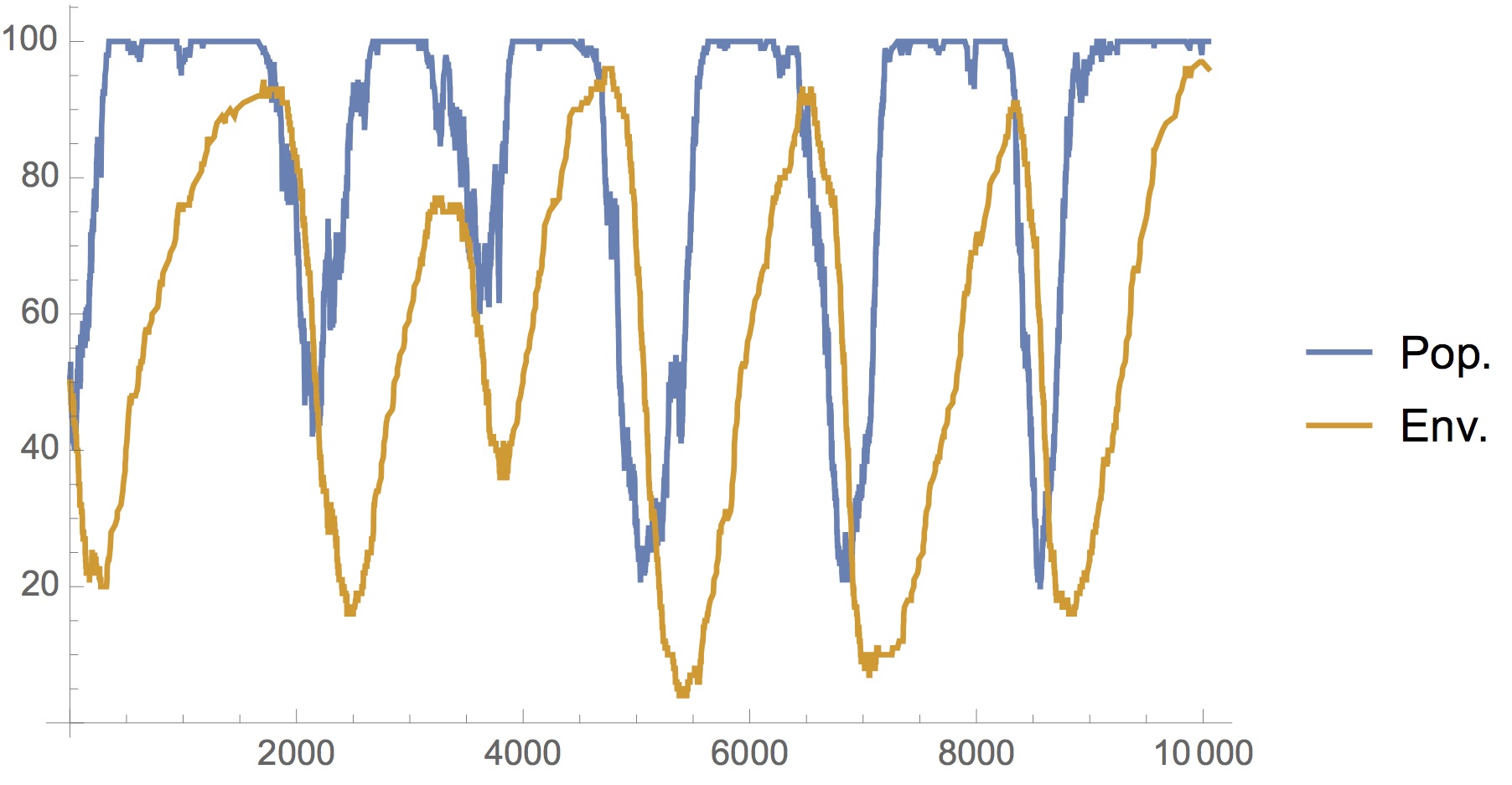
Interactions between individuals in a population can be complex, and may depend on the current state of the population. The framework of evolutionary game theory has been developed to capture these scenarios and their emergent phenomena. I approach this problem from two sides: Firstly, it is a playground for combining methods from mathematics and physics to arrive at an improved understanding. Secondly, I like to bring the problem (a little bit) closer to reality, by considering the impact of environmental variation and non-constant populations.

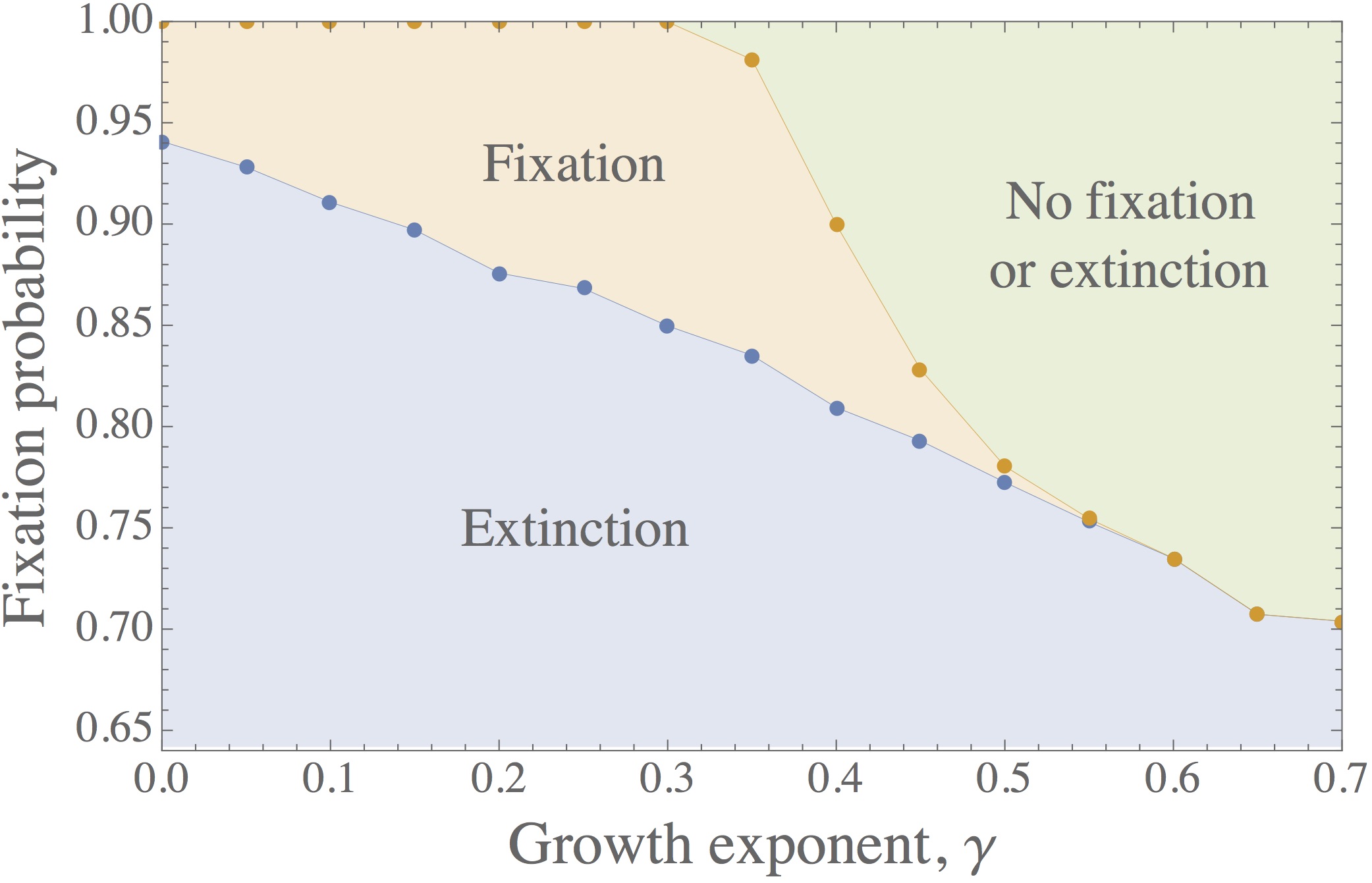
→ Analytical methods and approximations for mutant number distributions.
→ Lifetimes in individual-based processes.
→ Combining environmental and population dynamics.
→ …

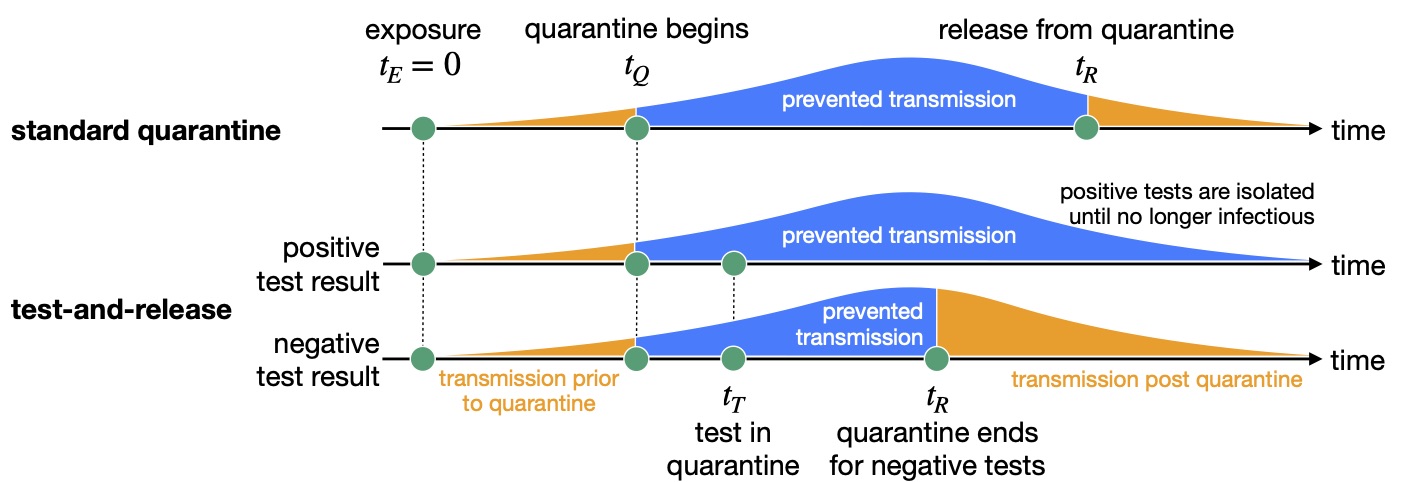
There is ongoing debate about the appropriate duration of quarantine, particularly since the fraction of individuals who eventually test positive is perceived as being low. We use empirically-determined distributions of incubation period, infectivity, and generation time to quantify how the duration of quarantine affects onward transmission from traced contacts of confirmed SARS-CoV-2 cases and from returning travellers. We also consider the roles of testing followed by release if negative (test-and-release), reinforced hygiene, adherence, and symptoms in calculating quarantine efficacy. We show that there are quarantine strategies based on a test-and-release protocol that, from an epidemiological viewpoint, perform almost as well as a 10 day quarantine, but with fewer person days spent in quarantine. The findings apply to both travellers and contacts, but the specifics depend on the context.

This methodology has been used by the Swiss COVID-19 Science Task Force in policy briefs relating to quarantine duration, cost, and strategy comparison as well as by the European Center for Disease Control (ECDC) for their air travel quarantine guidance. From 08.02.2021, the seven day test-and-release strategy will be used in Switzerland.

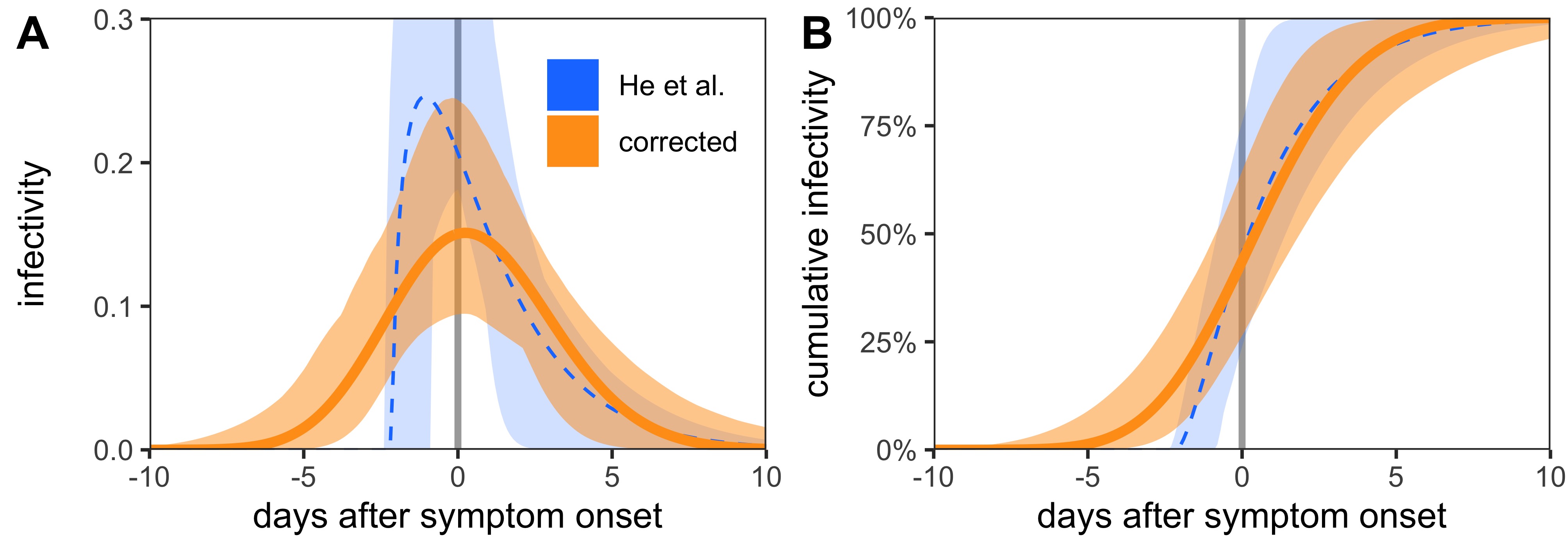
The infectivity profile describes infectiousness relative to symptom onset time. In He et al. Nat. Med. (2020), it was calculated from the empirical serial interval distribution and incubation period distribution. However, I discovered a critical error in the code which, when corrected, resulted in a very different infectivity profile.

This story was covered by NZZ am Sonntag. Eventually a formal correction was made to the He et al. article.

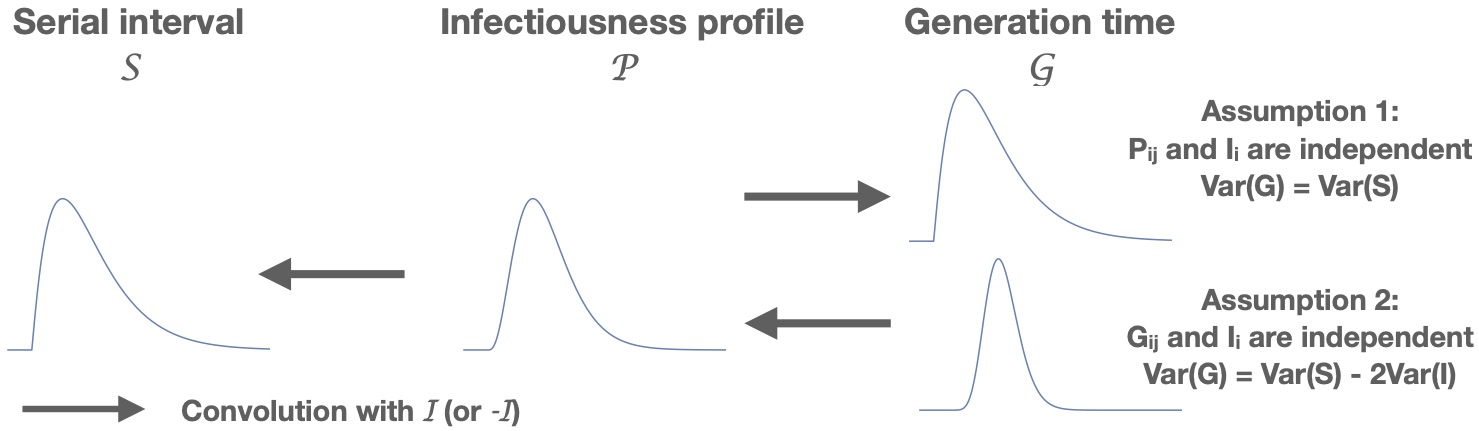
The generation time distribution, a critical factor in the dynamics and controllability of an epidemic, is often estimated based on the serial interval distribution (distribution of time intervals between symptom onset of an infector and an infectee). The different approaches to this calcuation make different -- and not always explicitly stated -- assumptions about the relationship between infectiousness and symptoms, resulting in different generation time distributions with the same mean but unequal variances. Here, we clarify the assumptions that each approach makes.

icumonitoring.ch is a platform to follow in near-real time beds/ventilators occupancy in intensive care units (ICU) in Switzerland during the COVID19 epidemic. The platform offers projections of ICU occupancy 3- and 7-days ahead by Regions, Cantons, and hospitals. This platform now features on SRF's COVID-19 platform.

I predict ICU bed occupancy in Switzerland due to the current COVID-19 pandemic. In particular, I quantify the risk of exceeding ICU capacity under different epidemic scenarios including a second wave of infections.